Método de Newton-modificado

O método de Newton aqui descrito é de forma rústica, ou seja, o seu código fonte é bem de iniciantes. Pois ainda estou aprendendo a linguagem de programação visando o cálculo numérico.

/**********************************************************************************/

#include

#include

#include

#define NI 1000

FILE*arquivo;

double xn,xv;

double f,df;

double newton(double xv){

xn=xv-f/df;

}

main(void){

int n;

arquivo=fopen("root2.dat","w");

xv=1;

for(n=0;n<=NI;n++){

f=4*cos(xv)-exp(xv);

df=-4*sin(xv)-exp(xv);

newton(xv);

fprintf(arquivo,"%d %.10f \n", n,xn);

printf("%d %.10f \n", n,xn);

xv=xn;

}

fclose(arquivo);

}

/**********************************************************************************/

Mapa de Hénon

Neste Post, trago a construção simples em C do mapa de Hénon, o algoritmo é bem básico, pois estou iniciando na linguagem de programação C.

A definição :

"O mapa Hénon é um sistema dinâmico a tempo discreto . É um dos exemplos mais estudados de sistemas dinâmicos que exibem comportamento caótico. Tal mapa leva um ponto (xn, yn) no plano para um novo ponto de descrito pelo sistema discreto de equações.

O mapa depende de dois parâmetros, a e b, o mapa Hénon canônicas têm valores de a = 1,4 e b = 0,3. Para estes valores apresenta caos. Para outros valores de a e b do mapa convergem para uma órbita periódica. O mapa foi criado por Michel Hénon. Para o mapa canônico, um ponto inicial do plano será tanto uma abordagem de um conjunto de pontos conhecido como o atrator Hénon, ou diverge para o infinito. Como um sistema dinâmico, o mapa Hénon canônico é interessante porque, ao contrário do mapa logístico, suas órbitas desafiam uma descrição simples."

O Código em C que trago aqui, é bem simples é apenas para fazer as iterações nas equações que descrevem o mapa de Hénon. Junto trago o script (.plt) do programa GNUPLOT, para a leitura dos arquivos formato ASCII, gerados pelo programa escrito em C com a extensão (.dat), também os comandos via terminal. Os valores de (a, b)= (1.2, 0.2); (1.3, 0.3) e (1.4, 0.3)

/*--script em C----*/
/*-------Bibliotecas------*/
#include
#include
#include
/*----escrita do arquivo .dat----*/
FILE*arquivo;
/*------inicio do programa-------*/
int main(void){
/*-----------Variaveis-----------*/
int n;
double xv,yn,xn,yv,a,b;
double x0,y0;
double c0,d0,cn,cv,dn,dv;
/*---------------------------------*/
arquivo=fopen("mapa_de_henon.dat","w");

/*---Parâmetros do mapa de Hénon---*/
a=1.2;
b=0.2;

/*---Condições iniciais aleaórias---*/
srand48(20100608);
x0=drand48();
y0=drand48();

for(n=0;n<=1000;n++){

xn=yv+1-a*pow(xv,2);

yn=b*xv; xv=xn;

yv=yn;

/*---escreve no arquivo .dat----*/

fprintf(arquivo,"%f %18f \n",xn,yn);

/*---escreve no terminal--------*/

printf("%d %f %18f \n",n,xn,yn);

}
fclose(arquivo); return 0; }
/*Fim do programa*/

O script para o GNUPLOT

reset
set title "Mapa de Hénon \n para a=1.4, b=0.3 ;"
set xlabel "Xn+1"
set ylabel "Yn+1"
plot 'mapa_de_henon.dat' using ($1):($2) t"" with points 3 6
replot pause -1 "Imagem PNG - Feche o Gnuplot completamente"
set output "mapa_henon.png"
set terminal png size 1024,748 pause -1 "Feche completamente o GNUPLOT"
replot =================================================================== As figuras A, B e C, são os gráficos gerados com os scripts acima, que representam os mapas de Hénon.

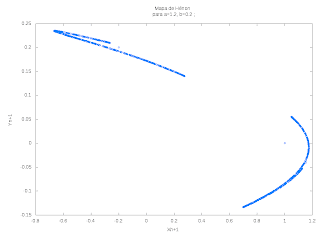
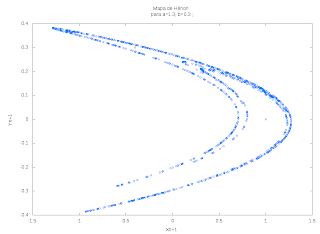
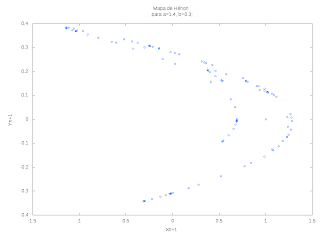
Os gráficos acima são resultados dos scripts criados em C e em GNUPLOT.

Pode se notar pelos gráficos as mudanças sensíveis dos parâmetros a e b nas equações do mapa de Hénon geram gráficos distintos com as mesmas condições inciais (xo, y0) que foram geradas aleatóriamente.

Os comandos via terminal para compilar o script em C:

gcc -g -o nomedoarquivo.x nomedoarquivo.c -lm

e em gnuplot

gnuplot nomedoarquivo.plt

Os arquivos em C após compilados será gerado um arquivo .dat que será usado na compilação com o gnuplot via terminal, gerando assim o gráfico e salvando em .png

Runge Kutta in C amateur

No momento tento implementar o método de Runge-Kutta de 4º Ordem para equações diferenciais, é um método meio rustico ainda, não está bem lapidado com uma escrita em C, bem organizada e legível. Uma justificativa é o fato de ser iniciante nesta linguagem.
Uma descrição do método de Runge- Kutta de 4º ordem, consiste em determinar constantes apropriadas tais que a fórmula:

yn+1=yn+ak1+bk2+ck3dk4

Que tenha uma certa concordância com um desenvolvimento de Taylor até h⁴ , isto é até o quinto termo. O resultado do método é dado pelas seguintes equações.

yn+1=yn+(k1+k2+k3+k4)/6

k1=h f(xn,yn)

k2=h f(xn+h/2, yn+k1/2)

k3=h f(xn+h/2, yn+k2/h)

k4=h f(xn+h, yn+k3)

Onde h é o passo dado no intervalo de integração, ou seja, se meu intervalo é [0;1] então com um h=0,2, o intervalo terá a seguinte sequência numérica {0, 0,2, 0,4, 0,6, 0,8, 1,0}.
O código fonte em C que trago aqui é para uma equação em específico. Ainda estou trabalhando em um código que eu somente coloque a função sem ter que modificar o código fonte.

Segue o código em C do Método de Runge Kutta, para a resolução da equação:

dy/dx = x-y (1)
ou
y'=x-y

/*********************************************************************/
/*Bibliotecas*/
#include
#include
#include
FILE*rk4;
/*Inicio do programa*/
main(){
rk4=fopen("rk4.txt","w");
int n;
double x,yv,h,yn,x0;
double f1,f2,f3,f4;

h=0.2;
x0=0;
yv=2;

for(n=0;n<=10;n++){
/*Variaveis do método dy/dx=x+y, aqui já na equação diferencial a ser integrada*/

f1=h*(x+yv);
f2=h*((x+h/2)+(yv+f1/2));
f3=h*((x+h/2)+(yv+f2/2));
f4=h*((x+h)+(yv+f3));

/* Escreve no terminal e no arquivo*/

fprintf(rk4,"%lf%18lf\n",x,yn);
printf("%lf%18lf\n",x,yn); }

/**** Escreve no terminal e no arquivo*****/

fprintf(rk4,"%lf%18lf\n",x,yn); printf("%lf%18lf\n",x,yn);

}
fclose(rk4); }

/*Fim do programa*/
/************************************************************************/

A solução algébrica da equação (1)

y(x)=3exp(x)-x-1 (2)

A seguir os gráficos da equação resolvida pelo método e algebricamente, apesar dos erros obtidos pelos calculos computacionais, podemos notar que o seu bom resultado gráficamente.

Gráfico calculado pelo método de Runge Kutta de quarta ordem














Gráfico obtido pela função exata calculada algebricamente.

Programa (2)

O código fonte aqui descrito neste post, é uma rotina para cálculos de volumes de esferas. Um código básico mas que pode ser util para quem esta aprendendo a implementar cálculos em linguagem C.

/*********Bibliotecas********/
#include
#include
/**************************/
/************Inicio do programa**************/
main(){
double V,r,pi,Vf,d;

pi=3.14159;
printf("Digite o raio da esfera:\n");
scanf("%lf",&r);
d=2*r;
V=(4/3)*pi*pow(r,3);
printf("Volume da esfera:%lf u.v\n",V);
Vf=pow(d,3)-(pi/6)*pow(d,3);
printf("Agora se imaginar extrair uma esfera de dentro de um cubo,\n o volume da figura:%lf\n",Vf);
return 0;
}
/************Fim do programa********************/

Linguagem C

Depois de tanto pesquisar sobre linguagens de programação optei pela qual o meu grupo de pesquisa trabalha, isso é devido a forças maiores. Explicações de quem a criou, desenvolveu é encontrado em qualquer site de busca como o Google. Aqui pra quem interessar é mais um blog de discussões da linguagem C aplicada a matemática e a física mais precisamente na dinâmica não-linear de sistemas complexos.

Aqui é uma rotina introdutória, com forma o tempo evoluir eu vou colocando mais.
A rotina a seguir é uma rotina que calcula o montante, um exemplo simples para matemática financeira, o compilador utilizado foi o GCC e o sistema operacional é o UBUNTU 10.04 (Lucid Lynx) que pode ser obtidos (aqui).

[rotina]

#include
#include

main(void)
{
int n;
float a,p,r,m;
printf("Digite o capital a ser investido:\n");
scanf("%f",&p);
printf("Digite a taxa que será aplicada:\n");
scanf("%f",&r);
{
printf("%4s%21s%20s\n","Tempo","Juro composto","Montante");
for(n=1;n<=10;n++)
{a=p*pow(1+(r/100),n);
m=p+a;
fprintf("%4d%21f%21f\n",n,a,m);
}
}
return 0;
}

Chuva

O que chove?
É chuva de vida
ou de pensamento?
Se chove tanto,
chovesse mais...
Mais que chuva,
mais que vento:
chovesse Céu.

Chovesse o Céu, eu voaria?
Ventaria feito papel?
Se eu voasse, nadaria?
Ou eu, pipa, levada ao léu,
da chuva me encharcaria,
à mesma força que me nasceu?

Que chuva chove?
Se é de vida,
chovesse o Céu!

{Célia de Lima}